| Introduction
Dans un premier temps, nous allons modéliser le didgeridoo par un cylindre dont le diamètre ne varie pas en fonction de la longueur. La simplicité du modèle permettra de comparer les résultats théorique avec les résultats expérimentales grâce à des didj cylindrique en PVC. Dans un 2ème temps, on modélisera le didj par un cône droit tronqué.
Le matériel nécessaire pour calculer la vitesse du son
- Un ordinateur
- Un tuner électronique : télécharger le logiciel dans la rubrique Télécharger
- Une calculatrice peut suffire ou une table de conversion note / fréquence.
- Un microphone
- Un didgeridoo
Calculer la conversion notes / fréquence
Une simple calculatrice permet de faire le calcul de la conversion notes/fréquence.
La note référence est le La avec une fréquence de 440 Hz, pour obtenir le La avec un octave en-dessous (en-dessus) on divise (multiplie) la fréquence par 2.
Un octave est divisé en 12 demi-tons. la rapport d'un demi-ton est racine douzième de 2 ou encore
12√2 équivaut approximativement à 1,05946
Exemple : On veut calculer la fréquence le Do d'un didgeridoo. on prend un La à 55Hz, il y a 3 demi-tons entre le Do et le La, et le Do est plus aigue que le La. On va donc multiplier 3 fois la fréquence du rapport avec le rapport pour obtenir le Do.
Ca donne
55 * (1,05946)3= 65,4 Hz pour la fréquence du Do d'un didgeridoo
Modélisation avec un didgeridoo cylindrique
Prenons comme modèle un didgeridoo cylindrique, la section S ( i.e. la surface de l'embouchure ou le pavillon du didgeridoo) ne varie pas en fonction de la longueur.
La formule qui lie la fréquence F en Hertz (s-1) avec la longueur (d'onde) du didgeridoo h en mètres et la vitesse C en m.s-1est la suivante.
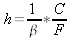 (1)
beta β est un paramètre qui dépend de la définition du système, d'un coté l'embouchure est fermé, et le pavillon est ouvert. D'après les règles vibratoires, alpha est égal à 4.
La vitesse du son est la suivante :
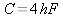 (2)
Valeurs expérimentales
Voici les valeurs mesurées avec des didgeridoo en PVC de référence, tout droit dont la section ne varie pas.
Les tests ont été faits dans une salle à 25°C.
Type de didj
| Diamètre intérieur
(en mètre)
| Longueur h (en mètre)
| Note trouvée
| Fréquence associée (en Hz)
| vitesse du son | | PVC | 0,037 | 1,047 | E | 82,5 | 345,51 | | PVC | 0,037 | 0,986 | F | 87,4 | 344,71 | | PVC | 0,037 | 1,103 | D# | 77,8 | 343,25 | | PVC | 0,037
| 1,568 | A | 55 | 344,96 | | PVC | 0,037
| 1,398 | B | 61,8 | 345,59 | | PVC | 0,037
| 1,177 | D | 73,5 | 346,04 | | PVC | 0,037
| 1,24 | C# | 69,3 | 343,73 | | PVC | 0,044 | 1,302 | C | 65,4 | 340,6 | | PVC | 0,051 | 1,32 | C+25%
| 67
| 348,48 | | PVC | 0,027 | 1,315 | C-15%
| 64,6
| 339,8 |
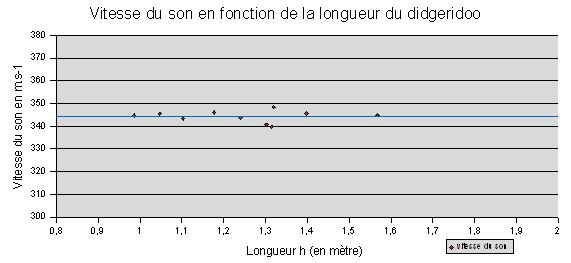
on trouve une moyenne de la vitesse du son à 344,3 m/s
Note : Le diamètre du didgeridoo n'influence pas la note comme on pourrait le croire dans la pratique, en revanche ça influence sur la jouabilité du didj.
La théorie du didgeridoo (modélisation cônique)
La modélisation d'un didgeridoo cônique fait intervenir 3 paramètres : le diamètre de l'embouchure Di ( ou le rayon Ri=Di/2 ), le diamètre du pavillon Do ( ou le rayon Ro=Do/2 )et la longueur du didgeridoo. La modélisation consiste en une soustraction d'un volume d'un cône de longueur h+e et d'angle alpha par un autre cône de longueur e ayant le même angle alpha. On obtient un cône droit tronqué au niveau du sommet.
Posons les formules de bases
Le volume du cône tronqué est :
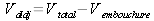 (3)
Le volume d'un cône est défini par :
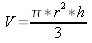 (4)
r est le rayon de la base en m
h est la hauteur du cône en m
La fréquence est définie par
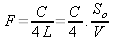 (5)
C'est la vitesse du son en m/s
So est la surface de sortie du didgeridoo en m2
V est le volume du didgeridoo
Les équations de la géométrie
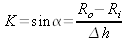 (6)
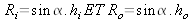 (7)
Résolution
En appliquant sur la formule (3) l'équation (4) on obtient
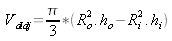 (8)
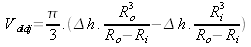 (9)
Ro est le rayon de la surface de sortie du didgeridoo en m
Ri est le rayon de la surface de l'embouchure du didgeridoo en m
en continuant on obtient
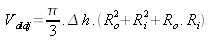 (10)
Finalement en appliquant (10) sur (5) on peut calculer la fréquence pour une vitesse de son donnée
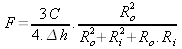 (11)
ou encore, on peut calculer la vitesse du son pour une note défini (par le tuner)
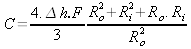 (12)
Les résultats expérimentales seront durs à vérifier car il est difficile de trouver des didgeridoo en PVC de forme conique.
la formule (11) permet de mettre en évidence l'influence de la hauteur de la note en fonction de la longueur du didgeridoo h, du rayon Ro et du rayon Ri . Voici les conséquences
Pour une taille du didgeridoo d'autant plus grande, la note est plus grave.
Pour une taille du didgeridoo d'autant plus petite, la note est plus aigue.
Pour une taille du pavillon d'autant plus grande, la note est plus aigue.
Pour une taille du pavillon d'autant plus petite, la note est plus grave.
Pour une taille de l'embouchure d'autant plus grande, la note est plus grave.
Pour une taille de l'embouchure d'autant plus petite, la note est plus aigue.
|